What do you understand by engineering antenna pattern? Explain the corresponding pattern
2. What do you understand by engineering antenna pattern? Explain the corresponding pattern.
Sum-and-Difference Patterns - Engineering Antenna Pattern:
After obtaining a predicted field-strength contour we can engineer an antenna pattern to conform to uniform coverage. Far different antennae pointing in different directions and with different spacings, we can use any of a number of methods. If we know the antenna pattern and the geographic configuration of the antennae, a computer program can help us to find the coverage. Several synthesis methods can be used to generate a desired antenna configuration.
General formula:
Many applications of linear arrays are based on sum-and-difference patterns. The main beam of the pattern is always known as the sum pattern pointing at an angle θo. The difference pattern produces twin main beams straddling θo. When 2N elements are in in array, equispaced by a separation d, the general pattern for both sum and difference is
For a sum pattern, all the current amplitudes are the same.
For a difference pattern, the current amplitudes of one side (half of the total elements) are positive and the current amplitudes of the other side (half of the total elements) are negative.
Most pattern synthesis problems can be solved by determining the current distribution In. A few solutions follow.
Synthesis of sum patterns:
Dolph-Chebyshev synthesis of sum patterns: This method can be used to reduce the level of sidelobes; however, one disadvantage of further reduction of sidelobe level is broadening of the main beam.
Taylor synthesis: A continuous line-source distribution or a distribution for discrete arrays can give a desired pattern which contains a single main beam of a prescribed beamwidth and pointing direction with a family of sidelobes at a common specified level. The Taylor synthesis is derived from the following equation, where an antenna pattern F(θ) is determined from an aperture current distribution g(l)
Symmetrical pattern: For production of a symmetrical pattern at the main beam, the current amplitude distribution g(l) is the only factor to consider. The phase of the current distribution can remain constant. A typical pattern (Fig.2.1a) would be generated from a current-amplitude distribution (Fig.2.1b).
Asymmetrical pattern: For production of an asymmetrical pattern, both current amplitude g(l) and phase arg g(1) should be considered.
Synthesis of difference patterns (Bayliss synthesis):
To find a continuous line source that will produce a symmetrical difference pattern, with twin main beam patterns and specified sidelobes, we can set
For a desired difference pattern such as that shown in Fig. 2.2a, the current-amplitude distributions g(l) should be designed as shown in Fig. 2.2b and the phase arg g(1) as shown in Fig. 2.2c.
Null-free patterns:
In mobile communications applications, field-strength patterns without nulls are preferred for the antennas in a vertical plane. The typical vertical pattern of most antennas is shown in Fig. 2.3a. The field pattern can be represented as
where u = (2a/λ)(cos θ — cos θn). The concept is to add all (sin Пu)/(Пu) patterns at different pointing angles as shown in Fig. 2.3a. K is the maximum signal level. The resulting pattern does not contain nulls. The null-free pattern can be applied in the field as shown in Fig. 2.3b.
%20Formation%20of%20a%20null-free%20pattern.PNG) |
| Null-free patterns (a) Formation of a null-free pattern |


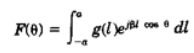
%20The%20aperture%20distribution%20for%20the%20twoantenna%20arrangement;%20(b)%20The%20evolution%20of%20a%20symmetrical%20sum%20pattern%20with%20reduced.PNG)

%20A%20modified%20Bayliss%20difference%20pattern;%20(b,c).PNG)

